Organo-Geometrica : The Theory And Practice Of Metaballs

In digital computer graphics "metaballs" are n-dimensional implicit surfaces. Instead of a defined object such as a sphere or a cube or a cylinder, metaballs behave as fields which will react with other metaballs, positive and negative. Two positive metaballs, for example, display surfaces which attract one another as they get closer, eventually coalescing into one object. A negative metaball, on the other hand, though invisible, will be seen to repel and deform the surface of a positive metaball.

Many computer graphics programs now have metaball modeling, rendering, and animation. The metaballs are often called by different names. All metaballs begin as spheres, with the surface marked as a threshold value. By deforming the spheres and manipulating the values of the positive and negative metaballs interacting with one another, one can render a theoretically limitless number of shapes, including even the inside of a cube, a cylinder, or a flat surface. When the metaball collections are carefully planned and animated, many stiking new virtual events may be displayed.

A metaball disc, for example,will react with other metaballs of the same construction in interesting ways.

Another unusual trait of metaballs is that in those progams which allow texturing, the texturing of the various metaballs, both positive and negative, will react with the texturing of other metaballs with which they are in contact.

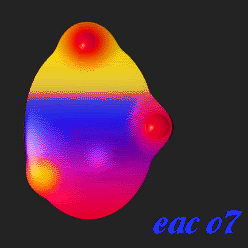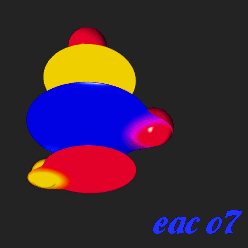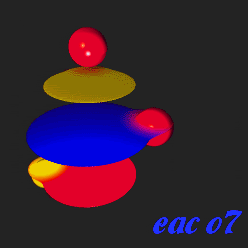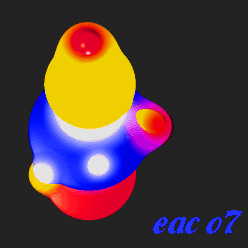
This allows effectively unlimited mixes and variations of textures even in those programs in which texture mixing is not otherwise possible.

By careful structuring of positive and negative metaball shapes and the mixing of textures, one opens new worlds of visual representation. Strictly speaking, what is visualized is a representation of mathematical events, though many of them seem to have analogues at the microscopic or submicroscopic level in physics, chemistry, biochemistry, and biology.

The commonplace is to describe metaballs and metaball modeling as "organic", as if there were something more organic about implicit and interactive surfaces than there is about the defined surfaces of a cube or pyramid or sphere, which are considered geometric. There is no question that there is a seemingly organic aspect at the macroscopic level.

Another way to characterize metaball stuctures and behavior, however, is to see them as analogues of the fields posited, though never actually seen directly, with electromagnetism, thermodynamics, and even in relativistic physics and astronomy.


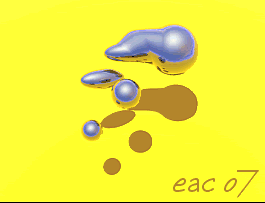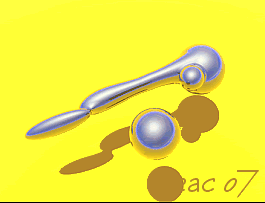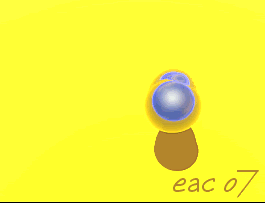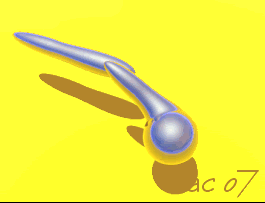
[copyright eac 07-09]
______________________________________________________________________________________
N.B: All of the above images are in Animated .GIF, the only animation file type universal to all browsers. Each is part of the series, "Cheerios", which was displayed at another site from 2007 onwards but which has now been taken down due to a change in software.